Analog Circuits

Lesson 1.3: Capacitors (Caps)

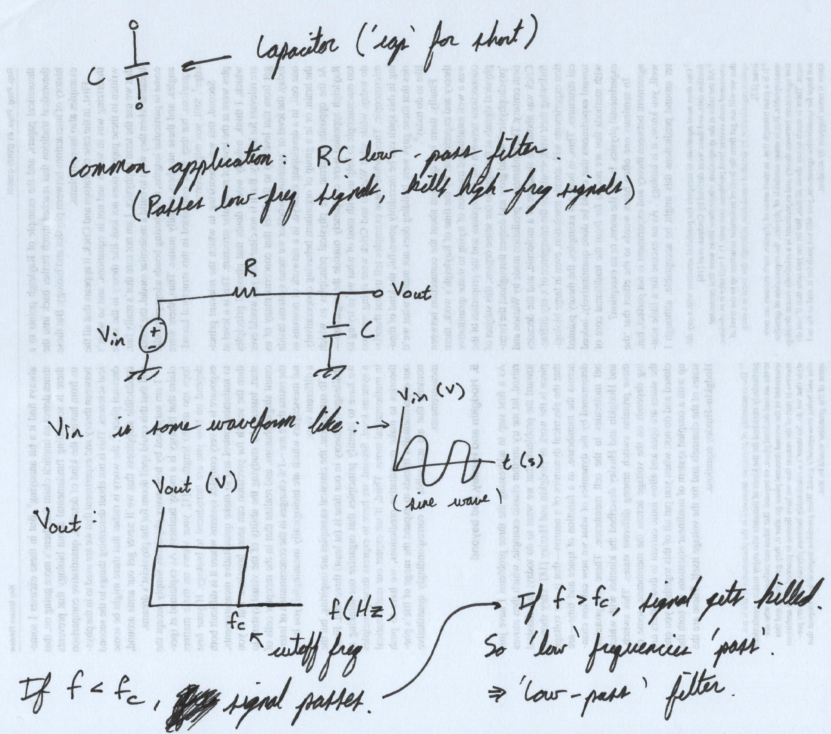
deriving the current-voltage relationship

Here's another one of those experimental laws from physics you just have to accept. You can prove it for yourself if you like, but you'll probably end up with the same conclusion. The law for capacitors is

\( q = C V \)

The variables are \( q \) for the charge on the plates of the capacitor, \( C \) for the capacitance, and \( V \) for the voltage across the capacitor.

We're circuit designers, so who cares about charge? That's an electromagnetic/photonic engineer's problem. We're more interested in what the current through the capacitor looks like. That's because the average charge flow rate (the current) is what matters, not exactly what that charge is. This becomes more important when you have to deal with AC circuits. The amount of charge moving through the circuit varies at different times, but the overall current remains constant.

If you take the time derivative of both sides, you get

\( \frac{dq}{dt} = C \frac{dV}{dt} \).

(We assumed the capacitance \( C \) was a constant here. You can get away with this in circuits that have only constant-valued capacitors in them. No variable capacitors allowed!)

Current is defined as the charge flow rate, \(I = \frac{dq}{dt} \), so we end up with

\( I = C \frac{dV}{dt} \)

We'll only use this formula in passing, because we're usually interested in how the circuit behaves at different frequencies. We can use complex numbers to avoid taking tons of time derivatives, so we'll derive a purely algebraic formula at the end of Part 1.

You can use separation of variables (a differential equation solution technique) to solve for \( V \) here:

\( V = \frac{1}{C} \int_{0}^{\infty} I(t) dt + V(0) \)

where \( V(0) \) is whatever initial condition you have for the voltage. Again, you can use complex numbers here to save yourself a lot of work. This solution is only valid for times after  \( t = 0 \). That's why the integration limits look that way.

When you build things like integrators (in the op-amp section of the course), it's good to remember that you are actually taking an integral. It's more of an intuitive aid than a math aid (although it is mathematically correct). Like with the differential equation above, we can use some fancy algebra to avoid actually taking the integral.

Only one calculation for this formula!

You most likely won't be asked to take the time derivative of some voltage function. That is, unless your professor wants to make sure you can still do time derivatives.

You might be asked to do a finite-difference approximation to find the current. That means you'll get two measurements for the voltage at two specific times. Then you subtract one from the other, as if you took a derivative. The formula for this is

\( I = C \frac{\Delta V}{\Delta t} = C \frac{V_2 - V_1}{t_2 - t_1} \).

Bottom line. The capacitor current-voltage equations in the time domain are \( I = C \frac{dV}{dt} \) and \( V = \frac{1}{C} \int_{0}^{\infty} I(t) dt + V(0) \).