Analog Circuits

Lesson 1.8: Series and Parallel Impedances

These are shortcuts for applying KVL and KCL that really simplify circuit problems.

We're allowed to derive the rules for resistors alone. Recall that this generalizes to any arbitrary impedance if you replace R with Z (we discussed this in Lesson 5).

We'll use induction to derive the rules for an arbitrary number of resistors using KVL and KCL.

Series Impedances

We'll use KVL and Ohm's Law to find the input resistance of this resistive circuit. Ultimately, we want to solve for R in Ohm's Law, but we have to specialize it to the circuit we're interested in.

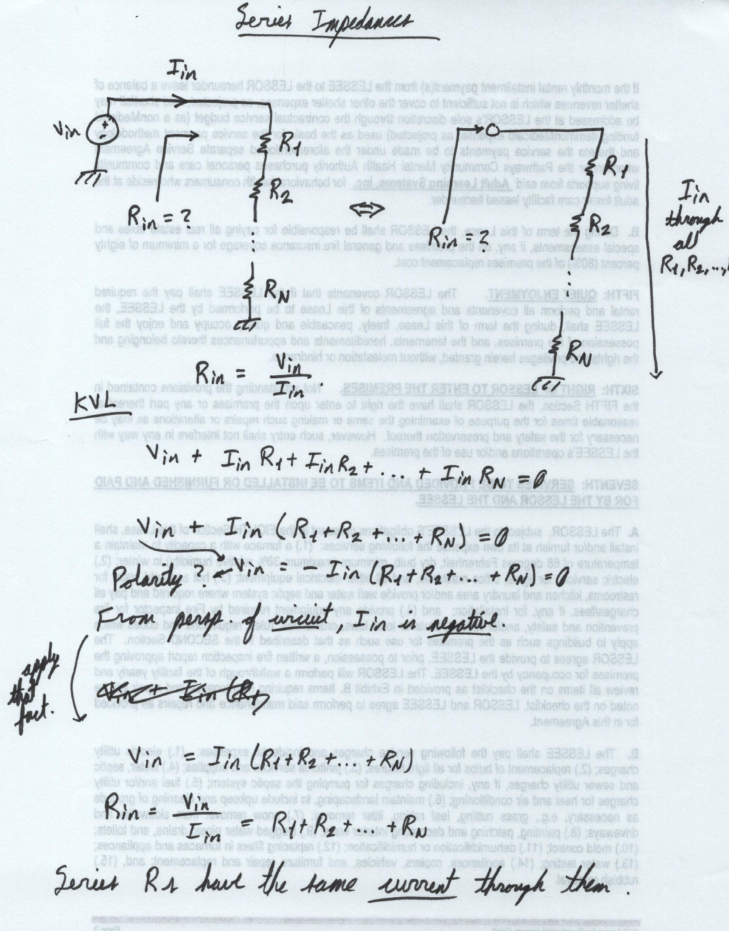
We call impedances with the same current through them series impedances. The input resistance formula for series impedances is \[R_{in} = R_1 + R_2 + ... + R_N. \]

Parallel Impedances

Same idea as with series impedances, but we'll use KCL instead of KVL.

We call impedances with the same voltage across them parallel impedances. We also introduced a new mathematical operator: the parallel operator. It's just a convenient way of writing down two-story fractions like we see for \( R_{in} \). There is no physical meaning attached to the parallel operator. It's defined this way, for just two variables:

\[ a \parallel b = \frac{1}{\frac{1}{a} + \frac{1}{b}} = \frac{a b}{a + b}. \]

The input resistance formula for series impedances is \[R_{in} = R_1 \parallel R_2 \parallel ... \parallel R_N. \]

Bottom line. Impedances in series have the same current through them. Impedances in parallel have the same voltage across them. Know the expressions for series and parallel impedances. Know how the parallel operator is defined.